Minimax Game Trees, Part 1
(Up to Basic Computer Science : Data Trees)

[Part 1] [Part 2]

This essay is a detailed explanation of one of the most important data structures ever created for Game Artificial Intelligence. The minimax tree is at the heart of almost every board game program in existence.

The Minimax Game Tree is used for programming computers to play games in which there are two players taking turns to play moves. Physically, it is just a tree of all possible moves. For instance, take a look at the following minimax tree of all the possible first two moves of Tic-Tac-Toe (the tree has been simplified by removing symmetrical positions).

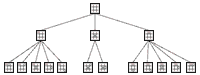
(Click this thumbnail to get the full-sized picture)

Notice that unlike other trees like binary trees, 2-3 tres, and heap trees, a node in the minimax game tree can have any number of children, depending on the game situation.

The tree above has three levels, but in programming, the levels of a minimax tree are commonly refered to as plies. At each ply, the "turn" switches to the other player. The two different players are usually refered to as Max and Min (these strange names will be explained shortly).

With a full minimax tree, the computer could look ahead for each move to determine the best possible move. Of course, as you can see in the example diagram, the tree can get very big with only a few moves, and to look even just five plies ahead can quickly overwhelm a simple computer. Thus, for large games like Chess and Go, computer programs are forced to estimate who is winning or losing by focusing on just the top portion of the entire tree. In addition, programmers have come up with all sorts of algorithms and tricks such as Alpha-Beta pruning, Negascout, and MTD(f) in order to lessen the number of nodes the computer must examine.

The minimax game tree, of course, cannot be used very well for games in which the computer cannot see the possible moves. In poker, for instance, the computer will have a very hard time judging what the opponent will do because the computer can't see the opponent's hand. So, minimax game trees is best used for games in which both players can see the entire game situation. These kinds of games, such as checkers, othello, chess, and go, are called games of perfect information.

The reason this data structure is named the minimax game tree is because of the simple algorithm behind the structure. Let us assign points to the outcome of a game of Tic-Tac-Toe. If X wins, the game situation is given the point value of 1. If O wins, the game has a point value of -1. Now, X will be trying to maximize the point value, while O will be tryiing to minimize the point value. So, one of the first researchers on the minimax tree decided to name player X as Max and player O as Min. Thus, the entire data structure came to be called the minimax game tree.

This minimax logic can also be extended to games like chess. In these more complicated games, however, the programs can only look at the part of the minimax tree; often, the programs can't even see the end of the game because it is so far down the tree. So, the computer only look at a certain number of nodes and then stops. Then the computer tries to estimate who is winning and losing in each node, and these estimates result in a numerical point value for that game position. If the computer is playing as Max, the computer will try to maximize the point value of the position, with a win (checkmate) being equal to the largest possible value (positive 1 million, let's say). If the computer is playing as Min, it will obviously try to minimize the point value, with a win being equal to the smallest possible value (negative 1 million, for instance). In between values are for games in which one side has an advantage.

Minimax Game Trees, Part 2: The Simple Secret to Minimax